post id: 13401
    cats: 1
    out: 1
    tn: https://loremflickr.com/960/480/nature,sky,clouds?lock=13401
  

Let’s Make a Deal

Monty Hall var på 50-talet programledare för ett TV-program som hette “Let’s Make a Deal”. Som en del av programmet fick en deltagare välja en av tre stängda dörrar. Bakom en dörr fanns en fin vinst och bakom de andra dörrarna fanns en get för att visa att man hade valt fel.

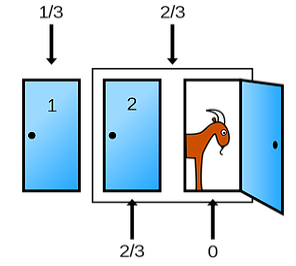
Det intressanta var att efter deltagaren hade valt dörr, men innan det hade avslöjats om man hade valt rätt, så öppnade Monty Hall först en av de andra två dörrarna. Hall, som ju visste vad som fanns bakom varje dörr, öppnade alltid en dörr med en get bakom. Alltså var nu två dörrar stängda och en med en get var öppen. Sedan ställde Hall frågan till deltagaren om han eller hon ville byta till den andra stängda dörren.

Vinner man något att byta dörr?

De flesta av oss känner nog att det inte skulle spela någon roll för chansen att vinna. Det känns kanske intuitivt som om det fortfarande borde vara 1/3-dels chans att vinna eftersom det fanns tre dörrar att välja på från början. Andra resonerar kanske att eftersom det bara är två dörrar kvar så borde chansen nu vara fifty-fifty och då kan man ju lika gärna hålla kvar vid den dörr man valde först.

Man har två tredjedelars chans att vinna!

De flesta blir förvånade av att höra att man alltid tjänar på att byta dörr.
Hur kan det komma sig?
Gå tillbaka till läget när alla dörrarna var stängda. När du gör ditt val är sannolikheten en tredjedel att du har valt rätt och därför alltså två tredjedelar att du har valt fel. När spelledaren sedan öppnar en av de två icke-valda dörrarna så är det fortfarande bara en tredjedels chans att du valde rätt första gången. Men det betyder att det är fortfarande också är två chanser på tre att att vinsten finns bakom någon av de två andra dörrarna. Och nu vet du ju vilken av de två dörrarna som det INTE är. Därför tjänar man statistiskt sett alltid på att byta.

Vad vi kan lära oss av Monty Hall-problemet

Var det uppenbart för dig att du borde byta dörr? Grattis!
Då har du en mycket bättre känsla för sannolikhet än de flesta. Även vissa professorer i matematik har varit svåra att övertyga om lösningen på Monty Hall-problemet.

Man kan ju undra varför detta är ett problem som kan vara bra att förstå sig på. Det är ju inte speciellt troligt att någon av oss kommer att bli inbjuden till en amerikansk TV-show från femtiotalet. Men en lärdom att ta med sig från Monty Hall-problemet är insikten om att vi människor har väldigt svårt för vissa typer att matematiska problem. Sannolikhetsproblem är intuitivt ofta väldigt svåra för oss att bedöma, och detsamma gäller också höga tal.

Detta gör att Monty Hall-problemet inte bara är en kul tankenöt att knäcka. Det kan också tjäna som en påminnelse om att man bör vara skeptisk till hur bra man är på att bedöma chanserna att vinna på spel eller att identifiera hur stor risk en investering har. Om det gäller stora summor är det bäst att räkna noga på saken först.

Länkar:
Monty Hall-problemet (Wikipedia)

Skeptisk måndag med VoF
Varje måndag publicerar vi ett blogginlägg om ett ämne som berör våra intresseområden, dvs vetenskap, pseudovetenskap, myter eller konspirationsteorier.